f fonksiyonunun türevi:
$f$ fonksiyonunun türev kuralı $$f^\prime(x)=3x^2$$ olur.
Fonksiyon üzerinde olan bir noktadaki teğet denklemi:
$a$ bir gerçel sayı olmak üzere $f$ fonksiyonunun $a$ noktasındaki teğet eğimi $3a^2$ olur ve bu teğet doğrusu $(a,a^3)$ noktasından geçer.
Dolayısıyla $f$ fonksiyonunun $a$ noktasındaki teğetinin denklemi $$y-a^3=3a^2(x-a) \ \ \ \text{ yani } \ \ \ y=3a^2x-2a^3$$ olur.
(1,1) noktasından geçen teğetler için koşul:
$a$ bir gerçel sayı olmak üzere $f$ fonksiyonunun $a$ noktasındaki teğet doğrusu $(1,1)$ noktasından geçiyorsa teğet denklemini sağlar ve $$1=3a^2\cdot 1-2a^3 \ \ \ \text{ yani } \ \ \ 2a^3-3a^2+1=0$$ eşitliğini elde ederiz.
Polinomun köklerini bulmak için yöntem:
Tam katsayılı bir polinom için rasyonel köklerini bulmak için rasyonel kök savını kullanabiliriz. Bu sav ile sabit terimin bölenlerinin payda ve baş katsayının bölenlerin paydada olduğu kesirler ile ilgilenmemiz yeterlidir.
$2x^3-3x^2+1$ polinomu için bu sayılar $$1,\ -1,\ \frac12,\ -\frac12$$ değerleridir.
Polinomu çarpanlara ayırma:
Kontrol ettiğimizde $1$ ve $-1/2$ değerlerinin $2x^3-3x^2+1$ polinomunun kökleri olduğunu görürüz.
Kökler toplamı $3/2$ olduğundan $1$ çift kat bir kök olmalıdır.
Bu bilgilerle $$2x^3-3x^2+1=(2x+1)(x-1)^2$$ olarak çarpanlara ayrılabilir.
(1,1) noktasından geçen teğetler:
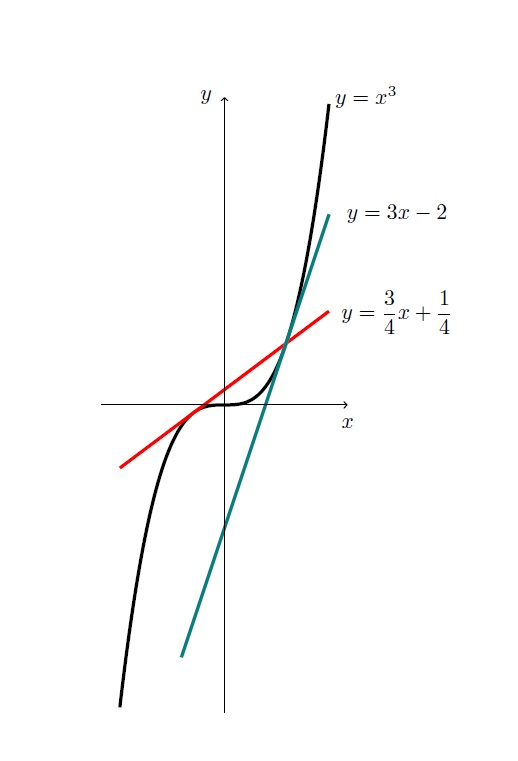
$f$ fonksiyonunun sadece $-1/2$ ve $1$ noktalarından geçen teğetleri $(1,1)$ noktasından geçer. Bu teğet denklemleri, sırası ile, $$y=\frac34x+\frac14 \ \ \ \text{ ve } \ \ \ y=3x-2$$ olur.