Yöntem:
Fonksiyonun artan olduğu aralıkları bulabilmek için türevinin pozitif olduğu aralıkları bulmamız gerekir. Bunun için
(1) Fonksiyonun türevini bulacağız.
(2) (Sürekli olan) türev fonksiyonumuzun sıfırlarını bulacağız.
(3) Bu bilgi ile sıfırlar arası işaretleri inceleyeceğiz.
(4) Pozitif işaretli olan yerler bize aralık üzerine bilgi verecek.
Fonksiyonun türevi:
$f$ fonksiyonun türev kuralı $$f^\prime(x)=5x^4\cdot e^{2x}+x^5\cdot 2e^{2x}= e^{2x}\cdot x^4\cdot (5+2x)$$ olur.
Türevi sıfır yapan değerler:
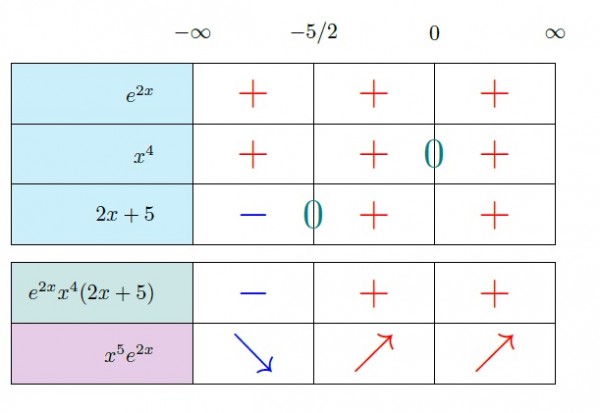
Çarpanları ayrı ayrı inceleyelim.
$e^{2x}$ her $x$ gerçel sayısı için pozitif değerler alır.
$x^4$ ifadesi sadece $x=0$ olduğundan sıfır değerini alır.
$5+2x$ ifadesi sadece $x=-5/2$ olduğundan sıfır değerini alır.
Türevin işaretini inceleme:
Çarpanları ayrı ayrı inceleyelim.
$e^{2x}$ her $x$ gerçel sayısı için pozitif değerler alır.
$x^4$ ifadesi $x<0$ ya da $x>0$ olduğunda pozitif değerler alır.
$5+2x$ ifadesi $x<-5/2$ olduğunda negatif, $x>-5/2$ olduğunda pozitif değerler alır.
Bu bilgileri birleştirsek
$x<-5/2$ olduğunda $f^\prime(x)$ değerleri negatif olur.
$-5/2<x<0$ olduğunda $f^\prime(x)$ değerleri pozitif olur.
$x>0$ olduğunda $f^\prime(x)$ değerleri pozitif olur.
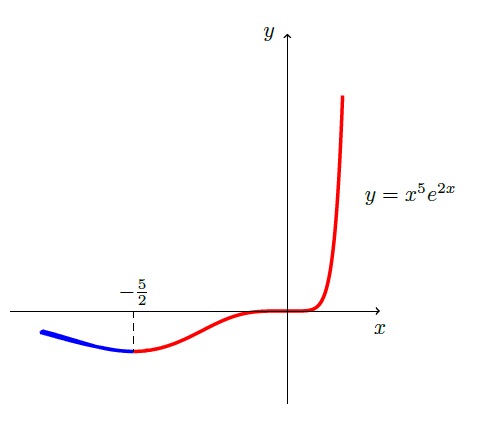
Fonksiyonun artan olduğu aralıkları bulma:
Ortalama değer savı gereği, $f$ fonksiyonu türevinin pozitif olduğu açık aralıkların kapalı aralıkları üzerinde artandır. Bu nedenle $$[-5/2,0] \ \ \ \text{ ve } \ \ \ [0,\infty)$$ kapalı aralıkları üzerinde $f$ fonksiyonu artan olur, ve bu ikisinin birleşimi olan $$[-5/2,\infty)$$ aralığı üzerinde de artan olur.
Ayrıca $f$ fonksiyonu $(-\infty,-5/2]$ aralığı üzerinde azalan olduğundan bu fonksiyonun artan olduğu biricik en geniş aralık $[-5/2,\infty)$ aralığı olur.