Sadeleştirmeler:
Her pozitif $t$ gerçel sayısı için $\sec^2 t=\tan^2 t+1$ eşitliği sağlanır. Ayrıca $t\in \left(-\frac\pi2,\frac\pi2\right)$ ise $$\sec t=\sqrt{1+\tan^2 t }$$ eşitliği sağlanır.
Her $x$ gerçel sayısı için $\arctan x\in \left(-\frac\pi2,\frac\pi2\right)$ olduğundan $$\sec (\arctan x)=\sqrt{\tan^2 (\arctan x)+1 }=\sqrt{x^2+1}$$ eşitliği sağlanır.
Geometrik olarak bu eşitliği görmek isterseniz aşağıdaki gibidir:
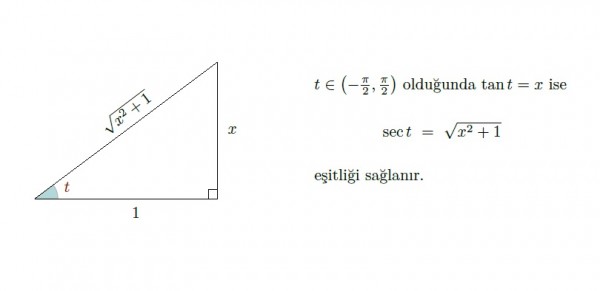
Burada negatif açılar olmasa da birim çembersel olarak x-eksenine göre simetri olduğundan eşitlik devam eder.
Fonksiyonun kuralını düzenleme:
Her $x$ gerçel sayısı için $$f(x) \ = \ \cos(\sec(\arctan x)) \ = \ \cos (\sqrt{x^2+1})$$ eşitliği sağlanır.
Zincir kuralına uygun yazma:
Zincir kuralını uygulayabilmek için fonksiyonumuzu halihazırda türevlerini bildiğimiz fonksiyonların bileşkesi olarak yazmamız gerekir. Bu amaç doğrultusunda
$f$ fonksiyonunun kuralını $$f(x)=\cos(\sqrt{x^2+1})=\underbrace{\left(\cos x\right)}_{f_3(x)}\circ\underbrace{\left(\sqrt x\right)}_{f_2(x)}\circ\underbrace{\left(x^2+1\right)}_{f_1(x)}$$ olarak yazabiliriz.
Bilgimizin olduğu türevler ve istenen türevin varlığı:
Gerçel sayılar üzerinde kuralı $\cos x$, pozitif gerçel sayılar üzerinde kuralı $\sqrt x$ ve gerçel sayılar üzerinde kuralı $x^2+1$ olan fonksiyonlar türevlenebilir fonksiyonlardır ve türevleri sırası ile
$-\sin x$, $\dfrac1{2\sqrt x}$ ve $2x$
fonksiyonlarıdır.
Bu türevler var olduğundan, zincir kuralı gereği, bu fonksiyonların bileşkesi olan $f$ fonksiyonu da gerçel sayılar üzerinde türevlenebilir.
Zincir kuralını uygulama:
Zincir kuralı gereği bu fonksiyonların bileşkesi olan $f$ fonksiyonu gerçel sayılar üzerinde türevlenebilir ve \begin{align*}f^\prime(x)\ &= \ \underbrace{2x}_{f_1^\prime(x)}\cdot \underbrace{\frac1{2\sqrt{x^2+1}}}_{f_2^\prime(f_1(x))}\cdot \underbrace{\left(-\sin(\sqrt{x^2+1})\right)}_{f_3^\prime(f_2(f_1(x)))}\\[15pt] &=\ -\frac{x\cdot \sin(\sqrt{x^2+1})}{\sqrt{x^2+1}}\end{align*} eşitliği sağlanır.