Verilen senaryoyu resmetme:
Uçağın kişiyi geçtikten sonra uçağın aldığı yola $x$ km ve uçak ile kişi arasındaki mesafeye $s$ km diyelim.
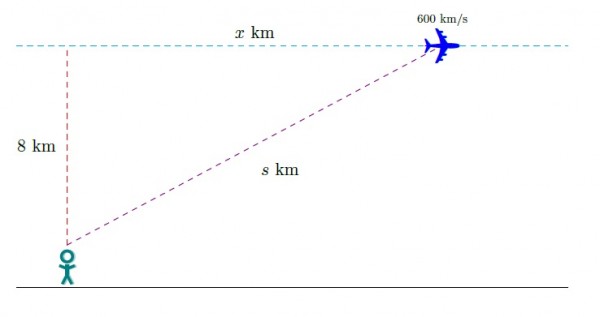
Verilen ve istenen:
Saat cinsinden $t$ zamanına bağlı olarak bu mesafeleri zamana bağlı fonksiyonlar olarak görebiliriz. Bize verilen $$\frac d {dt}x(t)=600 \text{ km/s}$$ olduğu ve istenen ise uçağın kişinin üzerinden geçişinden $90$ saniye (bu $1/40$ saat yapar) sonrasındaki $$\left.\frac {ds}{dt}\right|_{t=1/40}$$ değeridir.
Verilen ile isteneni bağlama:
Pisagor bağıntısı ile bir $t$ zamanında $$s^2(t)=x^2(t)+8^2$$ eşitliği sağlanır.
Kapalı fonksiyonun türevi ile $$2s\cdot \frac {ds}{dt}\ =\ 2x\cdot \frac {dx}{dt}$$ eşitliğini elde ederiz.
$t=90$ sn (yani $1/40$ saat) olduğunda $$\left.\frac {ds}{dt}\right|_{t=1/40}\ =\ \frac{x(1/40 )}{s(1/40)}\cdot \left.\frac {dx}{dt}\right|_{t=1/40}\ =\ 600\cdot \frac{x(1/40 )}{s(1/40)}$$ eşitliğini elde ederiz.
İhtiyacımız olan değerleri bulma:
$90$ saniye sonra uçak $$x(1/40)\ = \ 600\cdot \frac1{40} \ = \ 15 \text{ km}$$ yol alır ve Pisagor bağıntısı ile $$s(1/40)\ = \ \sqrt{x^2(1/40)+8^2}\ = \ \sqrt{15^2+8^2}\ = \ 17 \text{ km}$$ eşitliği sağlanır.
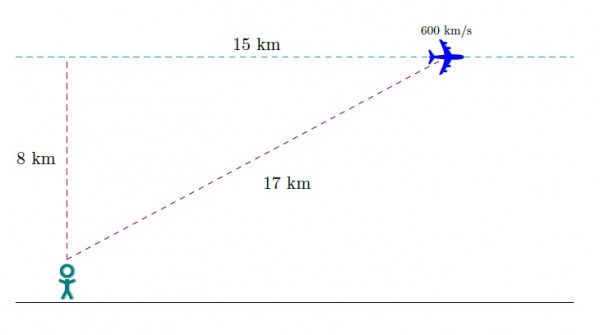
Sonuç:
Bu bilgiler ile birlikte $$\left.\frac {ds}{dt}\right|_{t=1/40}\ =\ 600\cdot \frac{x(1/40)}{s(1/40)}\ = \ 600\cdot \frac{15}{17} \ \approx \ 592.4 \text{ km/s}$$ eşitliğini elde ederiz.